Giải phương trình (1-2sinx)cosx/(1+2sinx)(1-sinx)=√3 kết quả chính xác chỉ trong vài bước, cùng tham khảo nhé!
Phương trình lượng giác cơ bản giúp bạn giải các bài toán trong sách giáo khoa toán, rèn luyện khả năng suy luận logic và logic, hình thành khả năng vận dụng các kết luận toán học trong cuộc sống và trong các môn học khác. Mời các bạn tham khảo cách giải phương trình mẫu: (1-2sinx)cosx/(1+2sinx)(1-sinx)=√3 dưới đây.

(1-2sinx)cosx/(1+2sinx)(1-sinx)=√3
Giải phương trình đã cho chi tiết như sau:
Điều kiện (1)
- 1+2sinx ≠ 0
- 1-sinx ≠0
(1-2sinx)cosx/(1+2sinx)(1-sinx)=√3⇔(1-2sinx)cosx = √3(1+2sinx)(1-sinx)
⇔ cosx – 2sinx.cosx = √3.(1 – sinx + 2.sinx – 2sin^2x)
⇔ cosx – sin2x=√3. (sinx+cos2x)
⇔ cosx – √3sinx = sin2x + √3cos2x
⇔ ½(cosx) – √3/2(sinx) = ½(sin2x) +√3/2(cos2x)
⇔ cos(x + π/3)=cos(2x – π/6)
⇔ có 2 trường hợp
- x + π/3 = 2x – π/6 + k2π ⇔ x = π/2 + k2π
- x + π/3 = -2x + π/6 + k2π ⇔ x = (-π/18) + k.(2π/3)
(Với k thuộc Z)
Kết hợp với điều kiện đã tìm (1) ở trên, nghiệm của phương trình là:
x = -π/18 + k(2π/3)
Vậy phương trình (1-2sinx)cosx/(1+2sinx)(1-sinx)=√3 có nghiệm là x = -π/18 + k(2π/3)
Các công thức lượng giác cơ bản

Đây là những công thức bắt buộc học sinh phải ghi nhớ để có thể làm được các bài tập lượng giác cơ bản nhất.
Bảng giá trị lượng giác của một số cung hoặc góc cụ thể
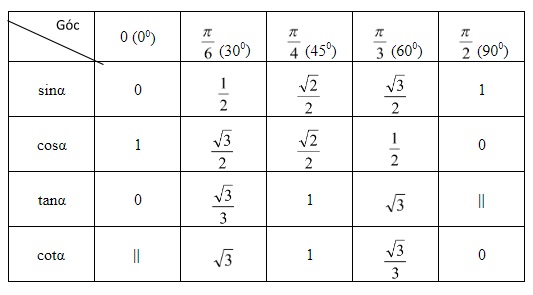
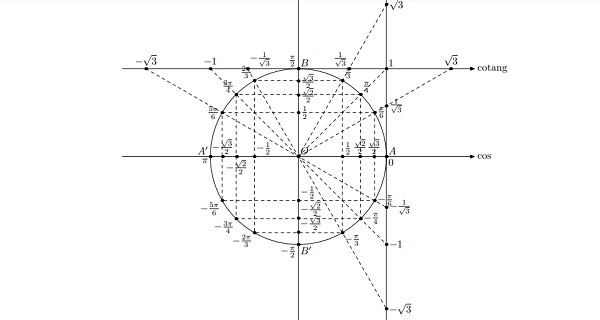
Hệ thức cơ bản :
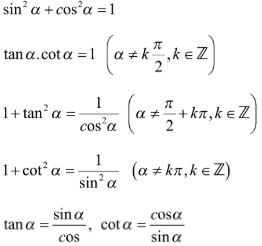
Cung liên kết
(cách nhớ: cos đối, sin bù, tan nhỏ hơn pi, phụ chéo)
Đây là những công thức toán về các góc có mối quan hệ đặc biệt như: đối nhau, phụ nhau, bù nhau, nhỏ hơn pi, nhỏ hơn pi / 2.
- Hai góc đối nhau
- cos (–x) = cosx
- sin (–x) = – sinx
- tan (-x) = – tanx
- cot (-x) = – cotx
- Hai góc kề bù
- sin (π – x) = sinx
- cos (π – x) = -cosx
- tan (π – x) = -tanx
- cot (π – x) = -cotx
- Hai góc nhỏ hơn π
- sin (π + x) = -sinx
- cos (π + x) = -cosx
- tan (π + x) = tanx
- cot (π + x) = cotx
- Hai góc phụ nhau
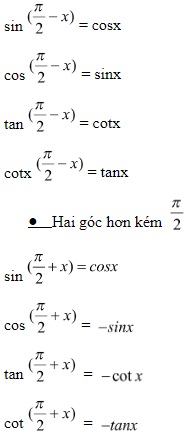
Công thức cộng và công thức nhân đôi
(cách nhớ: sin với sin cos cos, cos rồi cos cos sin sin dấu trừ, tan rồi chia cho mẫu số một trừ tan tan ):
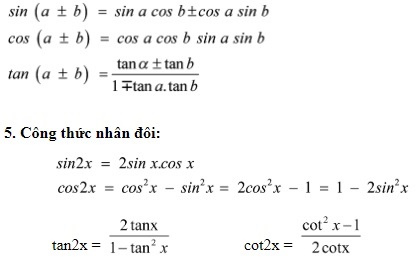
Công thức nhân ba:
- sin3x = 3sinx – 4sin3x
- cos3x = 4cos3x – 3cosx
Công thức hạ cấp:
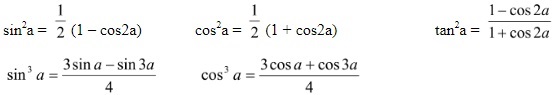
Công thức tính tổng và hiệu của sina và cosa

Công thức để chuyển đổi từ tích thành tổng :
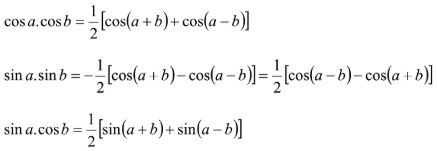
Cách ghi nhớ công thức lượng giác
Đối với nhiều học sinh, việc học các công thức lượng giác có thể được xem là rất khó. Dưới đây là một số cách ghi nhớ công thức lượng giác nhanh chóng và hiệu quả.
Cách ghi nhớ Công thức cộng
Cos + cos = 2 cos cos
cos – cos = trừ 2 sin sin
Sin + sin = 2 sin cos
sin – sin = sin 2 cos
Sin là sin cosine cosine
Cos, cos sin cos rồi trừ
Tổng số tiếp tuyến, sau đó tổng số tiếp tuyến
Chia 1 trừ cho tích tiếp tuyến, thật dễ dàng.
Cách ghi nhớ các giá trị lượng giác của các cung có liên quan đặc biệt
Cos đối, sin bù, chéo phụ, tan kém hơn pi
Cách ghi nhớ Công thức chuyển đổi tích thành tổng
Cos cos nửa cos- +, + cos-trừ
Sin sin nửa cos-trừ cos- +
Sin cos nửa sin- + + sin-trừ
Cách ghi nhớ Công thức chuyển đổi tổng thành tích
Cách nhớ của câu Tang mình + với tang ta, bằng sin 2 đứa trên cos ta cos mình… là
tanx + tany: tình mình cộng lại tình ta, sinh ra hai đứa con mình con ta
tanx – tany: tình mình trừ với tình ta sinh ra hiệu chúng, con ta con mình
Kết luận
Trên đây là cách giải phương trình lượng giác:
(1-2sinx)cosx/(1+2sinx)(1-sinx)=√3 với kết quả chính xác, cách giải dễ hiểu. Cùng những kiến thức và công thức liên quan. Hy vọng bài viết trên đây sẽ là một tài liệu giúp các bạn học lượng giác một cách thú vị hơn.
